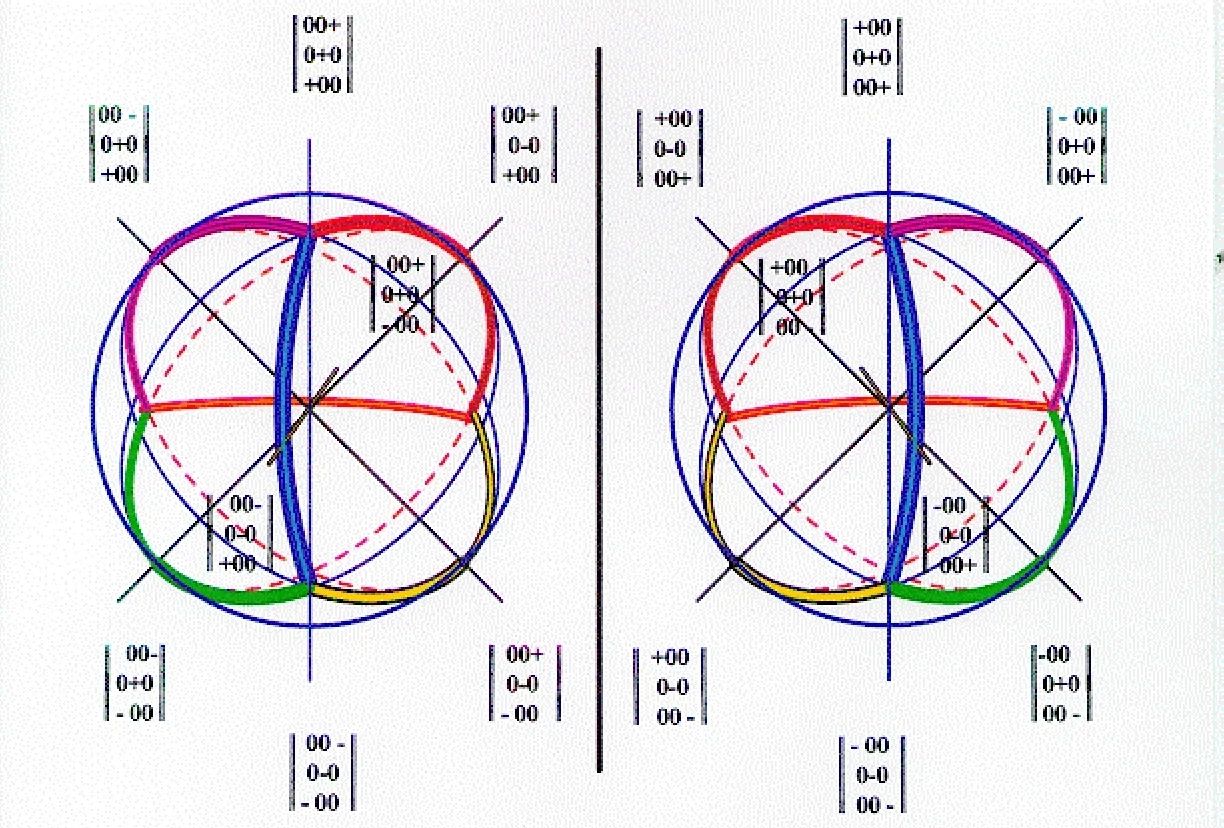
Our website opens with an Image of dual tetrahedra. Explore Hyper-Spherical Geometry in depth and discover how hyper-spherical geometry shapes our understanding of how G64 unifies the Platonic solids, starting with left-right tetrahedra duals. 

The first matrix illustrates the main diagonal and is defined as the identity, which means it does not change anything, when multiplied with another matrix. The second matrix is the mirror image of the first. We give a geometric meaning to the secondary diagonal, linking it to imaginary numbers, (numbers that are multiples of the square root of -1, used in advanced mathematics). Because there are two different forms of the tetrahedron, we suggest that there are actually six Platonic solids, grouped into three pairs of duals. g64 unifies platonic solids